A FCC (Fábrica de Cilindros de Carbono) fabrica vários tipos de cilindros de carbono. A FCC está instalada no décimo andar de um prédio, e utiliza os vários elevadores do prédio para transportar os cilindros. Por questão de segurança, os cilindros devem ser transportados na posição vertical; como são pesados, no máximo dois cilindros podem ser transportados em uma única viagem de elevador. Os elevadores têm formato de paralelepípedo e sempre têm altura maior que a altura dos cilindros.
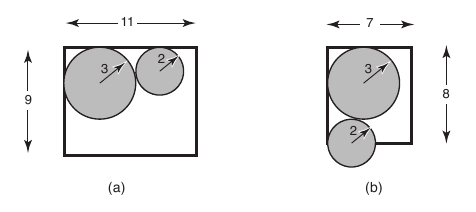
Para minimizar o número de viagens de elevador para transportar os cilindros, a FCC quer, sempre que possível, colocar dois cilindros no elevador. A figura abaixo ilustra, esquematicamente (vista superior), um caso em que isto é possível (a), e um caso em que isto não é possível (b):
Como existe uma quantidade muito grande de elevadores e de tipos de cilindros, a FCC quer que você escreva um programa que, dadas as dimensões do elevador e dos dois cilindros, determine se é possível colocar os dois cilindros no elevador.
Entrada
A entrada contém vários casos de teste. A primeira e única linha de cada caso de teste contém quatro números inteiros L, C, R1 e R2, separados por espaços em branco, indicando respectivamente a largura do elevador (1 ≤ L ≤ 100), o comprimento do elevador (1 ≤ C ≤ 100), e os raios dos cilindros (1 ≤ R1, R2 ≤ 100).
O último caso de teste é seguido por uma linha que contém quatro zeros separados por espaços em branco.
Saída
Para cada caso de teste, o seu programa deve imprimir uma única linha com um único caractere: ‘S’ se for possível colocar os dois cilindros no elevador e ‘N’ caso contrário.
| Exemplo de Entrada | Exemplo de Saída |
| 11 9 2 3 7 8 3 2 10 15 3 7 8 9 3 2 0 0 0 0 |
S N N S |
Dica
Podemos resolver diretamente alguns casos com uma verificação inicial simples: a menor dimensão da caixa, seja ela a largura ou a altura, deve ser suficientemente grande para que a circunferência de maior diâmetro possa ser colocada lá.
Devemos agora colocar as duas circunferências lado a lado, de modo que elas se tangenciam e tangenciam uma mesma aresta do retângulo dado. É nesta posição que elas ocupam o menor espaço possível, e a distância entre os centros é mínima. Seja R o segmento que liga os centros das circunferências (R=R1+R2). É fácil perceber que conseguimos construir um trapézio ligando os centros das circunferências à aresta que foi tangenciada. Desse trapézio, extraímos um triângulo retângulo cuja hipotenusa é justamente R.
Agora, podemos afastar as duas circunferências o máximo possível, colocando-as em extremidades diagonalmente opostas da caixa. Conseguimos construir um segundo trapézio ligando os centros a uma mesma aresta, e dele extrair um segundo triângulo retângulo de hipotenusa R′. O comprimento de R′ é a distância máxima, dentro da caixa, entre os centros das circunferências.
Se R′>R, os círculos cabem na caixa, e respondemos S. Se R′<R, temos que na situação de afastamento máximo existe uma interseção entre os círculos , ou seja, os círculos não cabem na caixa. Assim, respondemos N.
Dica retirada de: http://wiki.maratona.dcc.ufmg.br/index.php/ELEVADOR
Solução em C
#include <stdio.h>
#include <math.h>
int main() {
int l, c, r1, r2, maior;
char saida;
while ( scanf("%i %i %i %i",&l, &c, &r1, &r2) ) {
if(l == 0 && c == 0 && r1 == 0 && r2 == 0) { return 0; }
//o teste poderia ser: l+c+r1+r2 == 0
//como os numeros sao sempre positivos, nao teria problema
saida = 'N';
if (r1 > r2) {
maior = r1 + r1;
} else {
maior = r2 + r2;
}
if(maior <= l && maior <= c) {
if(sqrt(pow((l - r2 - r1), 2) + pow((c - r2 - r1), 2)) >= r1 + r2) {
saida = 'S';
}
}
printf("%c\n",saida);
}
return 0;
}
Teste o código: http://ideone.com/MW0fbR