Exercício cidades interligadas – complexo com matriz [incompleto]

Exercício bem interessante relacionado com a logística de transporte. Ele permite uma associação gráfica o que também é interessante, além de diversas partes, podendo ser selecionadas quais partes são de interesse (elas possuem nível de dificuldade variados).

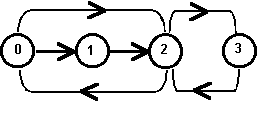
Considere n cidades numeradas de 0 a n-1 que estão interligadas por uma série de estradas de mão única. As ligações entre as cidades são representadas pelos elementos de uma matriz quadrada  L_nxn, cujos elementos l_ij assumem o valor 1 ou 0, conforme exista ou não estrada direta que saia da cidade i e chegue à cidade j. Assim, os elementos da linha i indicam as estradas que saem da cidade i, e os elementos da coluna j indicam as estradas que chegam à cidade j.

Por convenção l_ii = 1. A figura mostra um exemplo para n = 4.

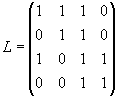
• A) Dado k, determinar quantas estradas saem e quantas chegam à cidade k.
• B) Dado k, verificar se todas as ligações diretas entre a cidade k e outras são de mão dupla.
• C) Relacionar as cidades que possuem saídas diretas para a cidade k.
• D) A qual das cidades chega o maior número de estradas?

#include <stdio.h>
#define TAM 4

int main() {
    int i, j, k, contIn=0, contOut=0, cont=0, contMaior=-1, cidadeMaior=-1;
    int L[TAM][TAM] = {1, 1, 1, 0,
                       0, 1, 1, 0,
                       1, 0, 1, 1,
                       0, 0, 1, 1};

    //A) Dado k, determinar quantas estradas saem e quantas chegam à cidade k.
    printf("Informe o numero da cidade (entre 0 e %d): ", TAM - 1);
    scanf("%d", &k);
    for (i = 0; i < TAM; i++) {
        if (k != i) { //desconsidera a própria cidade
            if (L[i][k] == 1) { contIn++; }
            if (L[k][i] == 1) { contOut++; }
        }
    }
    printf("%d estradas saem e %d estradas chegam\n", contOut, contIn);

    //B) Dado k, verificar se todas as ligações diretas entre a cidade k e outras são de mão dupla.
    for (i = 0; i < TAM; i++) {
        if (k != i) { //desconsidera a própria cidade
            if ((L[i][k] == 1) && (L[k][i] == 1)) {
                cont++;
            }
        }
    }
    printf("%d estradas de mao dupla\n", cont);

    //C) Relacionar as cidades que possuem saídas diretas para a cidade k.
    printf("Saidas diretas para a cidade: ");
    for (i = 0; i < TAM; i++) {
        if (k != i) { //desconsidera a própria cidade
            if (L[i][k] == 1) {
                printf("%i ", i);
            }
        }
    }
    printf("\n");

    //D) A qual das cidades chega o maior número de estradas?
    for (i = 0; i < TAM; i++) {
        cont = 0;
        for (j = 0; j < TAM; j++) {
            if (L[j][i] == 1) {
                    cont++;
            }
        }
        if (cont > contMaior) {
            contMaior = cont;
            cidadeMaior = i;
        }
    }
    printf("Cidade com maior numero de estradas: %d (com %d estradas)\n", cidadeMaior, contMaior-1);

    return 0;
}

================== Parte faltante do exercício ==============

E) Relacionar, se existirem cidades isoladas (cidades que não têm ligação com nenhuma outra) e cidades das quais não há saída.

F) Dada uma sequência de m inteiros cujos valores estão entre 0 e n-1, verificar se é possível realizar o roteiro correspondente. No exemplo dado, o roteiro representado pela sequência (m=5) 2 3 2 1 0 é impossível.

G) Dados k e p, determinar se é possível ir da cidade k para a cidade p pelas estradas existentes.

G.1) Qual o menor caminho entre as duas cidades?

H) Dado k, determinar se é possível, partindo de k, passar por todas as outras cidades apenas uma vez e retornar a k.