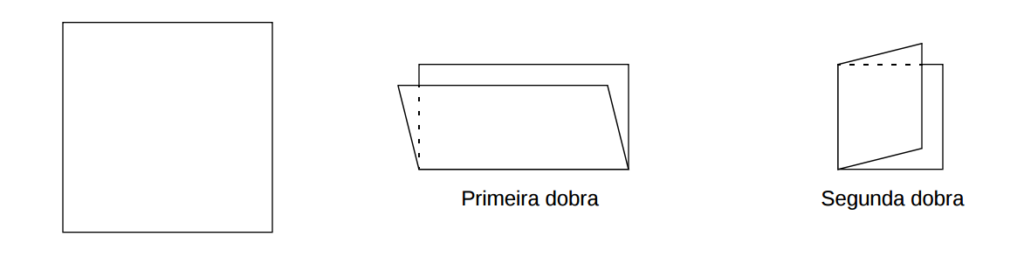
Zezinho tem aulas de Iniciação Artística em sua escola, e recentemente aprendeu a fazer dobraduras em papel. Ele ficou fascinado com as inúmeras possibilidades de se dobrar uma simples folha de papel. Como Zezinho gosta muito de matemática, resolveu inventar um quebra-cabeça envolvendo dobraduras. Zezinho definiu uma operação de dobradura D que consiste em dobrar duas vezes uma folha de papel quadrada de forma a conseguir um quadrado com 1/4 do tamanho original, conforme ilustrado na figura.
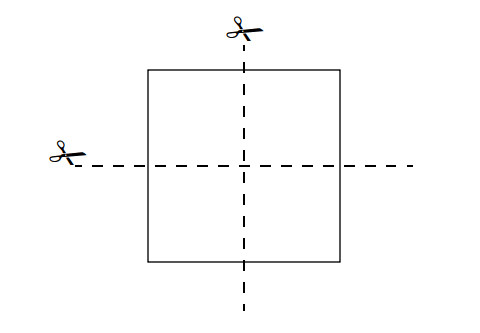
Depois de repetir N vezes esta operação de dobradura D sobre o papel, Zezinho cortou o quadrado resultante com um corte vertical e um corte horizontal, conforme a figura abaixo.
Zezinho lançou então um desafio aos seus colegas: quem adivinha quantos pedaços de papel foram produzidos?
Entrada
A entrada é composta de vários conjuntos de teste. Cada conjunto de teste é composto de uma única linha, contendo um número inteiro N (-1 ≤ N ≤ 15) que indica o número de vezes que a operação de dobradura D foi aplicada. O final da entrada é indicado por N = -1.
Saída
Para cada conjunto de teste da entrada seu programa deve produzir três linhas na saída. A primeira linha deve conter um identificador do conjunto de teste, no formato “Teste n”, onde n é numerado a partir de 1. A segunda linha deve conter o número de pedaços de papel obtidos depois de cortar a dobradura, calculado pelo seu programa. A terceira linha deve ser deixada em branco. A grafia mostrada no Exemplo de Saída, abaixo, deve ser seguida rigorosamente.
Restrições
-1 <= N <= 15 (N = -1 apenas para indicar o fim da entrada)
| Entrada | Saída |
| 1 0 -1 | Teste 1 9 Teste 2 4 |
Dica
Cada “dobradura D” dobra o papel duas vezes. Somente depois de dobrar o papel N vezes é que será feito o recorte do papel. Por isso que quando não se faz nenhuma dobradura (entrada zero), o resultado é que o papel recortado resultará em 4 pedaços.
Pode ser útil pegar um pedaço de papel e aplicar uma ou duas dobraduras D, recortar e contar os pedaços resultantes. Você verá que com uma dobradura D teremos 9 pedaços e com 2 dobraduras D teremos 25 pedaços.
Observe a evolução do número de dobraduras D e quantidade de pedaços resultantes:
0 = 4 pedaços
1 = 9 pedaços
2 = 25 pedaços
3 = 81 pedaços
4 = 289 pedaços
Solução C/C++
#include <stdio.h>
main(){
int n,teste=1,base,i,inc;
scanf("%d",&entrada);
while(n != -1){
base = 2;
inc = 1;
for(i=1; i<=n; i++){
base += inc;
inc *= 2;
}
printf("Teste %d\n",teste);
teste++;
printf("%d\n",base*base);
scanf("%d",&n);
}
}Na solução anterior eu mostrei uma forma de evoluir o resultado conforme o número de dobraduras D. Na a seguir eu troco a iteração realizada pela estrutura de repetição por um cálculo elaborado para determinar o resultado.
#include <stdio.h>
#include <math.h>
main(){
int n,teste=1;
scanf("%d",&n);
while(n != -1){
printf("Teste %d\n",teste++);
printf("%d\n",(int)(pow(4,n) + pow(2,n+1) + 1));
scanf("%d",&n);
}
}
Teste o código em: https://ideone.com/TaksNv