Tutorial sobre o trabalho: supervisory control architecture for discrete-event systems

O objetivo de tutorial é explicar o artigo de [1] com um passo-a-passo mais detalhado com a solução apresentada no trabalho.

O sistema modelado é automatic guided vehicles (AGV) que atende a uma célula de manufatura. O sistema é originário de [2, Sec. 4.7] e seus modelos são apresentados no trabalho.

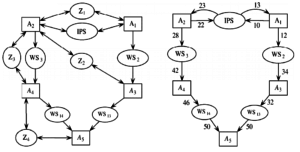
O sistema foi simplificado em [3], que utilizou a abordagem de control flow decomposition para tal. A figura abaixo mostra a simplificação realizada pelo control flow decomposition, que eliminou as especificações de controle Z1…Z4. A simplificação também levou a divisão do WS1 nas especificações W13 e W14. Isso porque o sistema será dividido em dois subsistemas (caminho da esquerda e caminho da direta).

Ao contrário do que aconteceu com WS1, o IPS1 e IPS2 foram juntados em uma especificação única IPS (ver mais adiante no modelo das especificações).

Plantas

As plantas d os 5 AGVs são mostradas a seguir.

Especificações

Diferente das especificações em [2], o trabalho de [1] somente marca os estados iniciais das especificações. Os modelos são mostrados abaixo.

Redução dos supervisores

O trabalho propõe a geração dos supervisores reduzidos para cada uma das especificações. O trabalho usa esses supervisores reduzidos para criar o controlador dos dois subsistemas, conforme:

Sub1 = A1 || A3 || A5 || WR2 || WR13 (140)

Sub2 = A2 || A4 || A5 || WR3 || WR14 (330)

Sendo, WRi os supervisores reduzidos para cada WSi.

Eu optei por fazer os SupC para gerar os supervisores. O resultado é o mesmo mas com menor processamento. Fiz isso também porque utilizando a ferramenta DESTool, não foi possível gerar todos os supervisores reduzidos devido a complexidade envolvida em alguns.

Sub1 = SupC(A1 || A3 || A5, WR2 || WR13)

Sub2 = SupC(A2 || A4 || A5, WR3 || WR14)

O resultado é o Sub1 com 140 estados e o Sub2 com 330 estados.

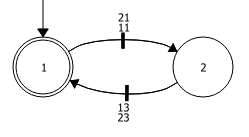
Veja que a especificação IPS não está presente nem em Sub1 nem em Sub2. Essa especificação associa os dois subsistemas e foi gerado um controlador somente para ela. Inicialmente é gerado um controlador com as plantas A1 e A2 que são associadas a especificação e depois esse supervisor é reduzido.

IPR = reduce( SupC(A1 || A2, IPS) )

O resultado é o autômato IPR mostrado abaixo.

Se for avaliado o conflito entre Sub1 e Sub2 ele não existe. O conflito aparece quando o supervisor IPR é adicionado. O trabalho então explora a inclusão de um outro supervisor que deve atuar juntamente com os outros 3, sendo esse novo supervisor o responsável por resolver o conflito, atuando como um coordenador.

Gerando o resolvedor do conflito

É preciso inicialmente identificar todos os eventos compartilhados entre os subsistemas. A interseção dos eventos de Sub1 e Sub2 mostra que os eventos de A5 estão presentes ({50, 51, 52, 53}). Também são adicionados os eventos de IPS ({11, 13, 21, 23}) que é o controle que gera o conflito.

Com esse conjunto de eventos ({11, 13, 21, 23, 50, 51, 52, 53}) é feito a projeção de Sub1 e Sub2 e que geram Int1 e Int2, respectivamente. Dessa operação serão gerados dois autômatos com 30 estados cada.

No DESTool, é preciso marcar a opção “minimal realisation” no momento da projeção. Essa opção irá fazer a projeção e também a minimização do autômato.

Os passos realizados apenas diminuem os supervisores e ainda não resolvem o conflito o que pode ser visto testando o bloqueio da composição síncrona dos supervisores (essa composição gera um autômato com 171 estados).

IntIP = Int1 || Int2 || IPR

O próximo passo consiste em calcular um novo supervisor a partir do IntIP. Esse novo supervisor utiliza uma especificação chamada “All” que consiste de um único estado com todos os eventos de IntIP em selfloop. Esse novo supervisor, chamado CS, elimina os bloqueios existentes em IntIP.

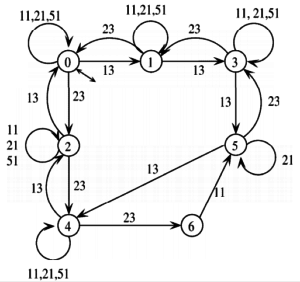
O supervisor CS possui 165 estados, mas pode também ser reduzido para simplifica-lo. Esse supervisor é o coordenador e resolve o conflito entre os demais supervisores. O autômato do coordenador é chamado de CR. Infelizmente o DESTool não consegue gerar o supervisor reduzido então é preciso utilizar o TCT no cálculo. O artigo apresenta como CR o autômato abaixo.

Quando eu fiz o processo obtive o autômato com uma pequena diferença: o meu autômato CR não possui o evento 51, mas esse evento não faz diferença no resultado final.

Para testar que não existe mais conflito no sistema utilizando esse coordenador é preciso fazer a composição síncrona entre os subsistemas e o coordenador e verificar que não existe conflito.

Teste = Int1 || Int2 || IPR || CR

O resultado é um autômato com 165 estados e não existência de bloqueio no autômato, mostrando que o coordenador resolve o conflito.

Tenha acesso aos modelos no software DESTool através da minha postagem disponível aqui.

Referências

[1] Feng, L., & Wonham, W. M. (2008). Supervisory control architecture for discrete-event systems. IEEE Transactions on Automatic Control, 53(6), 1449-1461.

[2] W. M. Wonham, “Supervisory control of discrete-event systems,” Dept. Electr. Comput. Eng., Univ. Toronto, Toronto, ON, Canada, 2001–2007 [Online]. Available: http://www.control.toronto.edu/DES, updates posted annually

[3] L. Feng and W. M. Wonham, “Computationally efficient supervisor design: Abstraction and modularity,” in Proc. 8th Int. Workshop Discrete-Event Syst., S. Lafortune, F. Lin, and D. Tilbury, Eds., Ann Arbor, MI, Jul. 2006, pp. 3–8